Wirkleistung (W)
Blindleistung (VAR)
Kompensation
| Wirkleistung |
Wirkleistung ist
die Energie, die tatsächlich in andere Energieformen umgewandelt wird
und die der Verbraucher
etwa als Bewegungsenergie, Wärme oder Licht nutzen kann. Also die tatsächlich genutzte Leistung. |
| Blindleistung | Blindleistung baut
elektrische oder magnetische Felder auf und ist erforderlich, um die Wirkleistung zu
übertragen. Kann aber nicht genutzt werden und ist eher hinderlich . Sie fließt im Stromnetz zwischen Erzeuger und Verbraucher hin und her, lässt sich aber nicht in andere Energieformen umwandeln. Sie belastet aber die Stromleitung, die auch für diese zusätzliche Blindleistung ausgelegt sein muss. |
| Scheinleistung | Die Scheinleistung setzt sich aus der Wirkleistung und der Blindleistung zusammen. Sie bezeichnet den gesamten im Stromnetz bereitgestellten Strom, von dem ein bestimmter Anteil – die Blindleistung – aber nicht verbraucht werden kann |
Wird ein Verbraucher an einer
sinusförmige Spannungsquelle angeschlossen,so ergibt sich auf Grund der Spannungshöhe und des angeschlossenen Widerstand des Verbrauchers
ein fließender Strom.
Die Leistung die vom Widerstand verbraucht wird ergibt sich aus der Multiplikation von Spannung und Strom.
Die Einheit für die elektrische Leistung ist Watt (W).
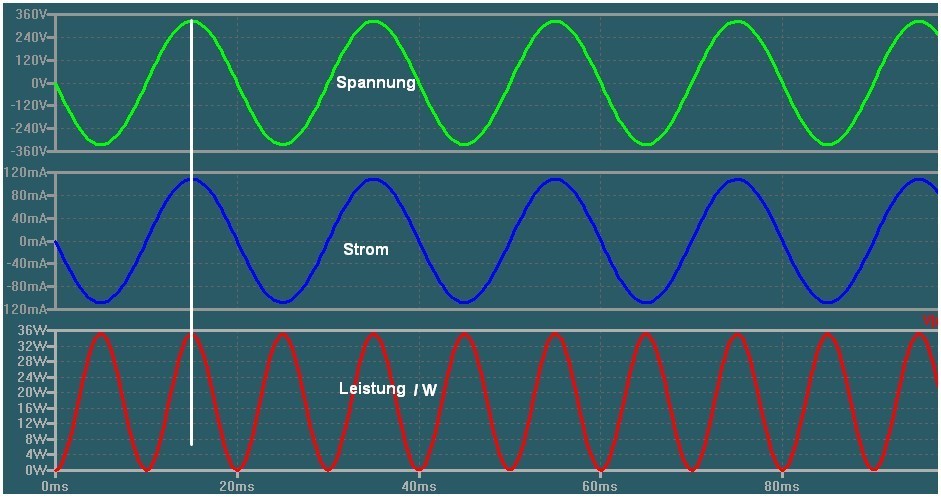
Sieht man sich die vertikale weiße Linie des nachfolgenden Oszillogramm an so ist die Multiplikation
aus Spannung und Strom zu diesem Zeitpunkt ca. 36 Watt (0,1A X 320 Volt).
Diese Leistung bezeichnet man als Wirkleistung und wird in Watt angegeben.
Wirkleistung ist die elektrotechnische Bezeichnung für eine Leistung die sich aus der Multiplikation von
Strom mal Spannung ergibt wenn keine Phasenverschiebung zwischen Strom und Spannung vorhanden ist.
Also wie hier im Beispiel dargestellt.
zwischen Spannung und Strom hervor rufen.
Man spricht dann von einer Phasenverschiebung.Das ist fast immer dann der Fall wenn es Verbraucher gibt die Kapazitiv oder Induktiv wirken.
Das es nur fast immer, aber nicht immer so ist wird etwas weiter unten erläutert.
Also wenn Kondensatoren oder Spulen verbaut sind wird einhergehend eine Phasenverschiebung hervorgerufen.
Spulen befinden sich beispielsweise in allen Stecker Netzteilen, Motoren , Vorschaltgeräte für Halogen Leuchten usw.
Auch Kondensatoren findet man in den meisten Haushaltgeräten.
Fast immer dann wenn diese Teile verbaut sind befindet sich zwischen Spannung und Stromverlauf eine gewisse zeitliche Verschiebung
die für eine erschwerte Berechnung sorgen.
Der zeitliche Versatz kann bis zu 90° betragen.
Dabei gilt eine gesamte Sinuslinie als 360°
Hier sieht man eine Konstellation bei
der an statt eines Ohmschen Widerstand, ein Kondensator eingesetzt wurde.
Jetzt kommt es zu einer Phasenverschiebung zwischen Spannung und Strom .
Auf Grund dieser Verschiebung kommt es bei der Multiplikation von Spannung und Strom
nun zu völlig andere Werte.
Deutlich zu erkennen an der jetzt auch verschobenen Sinuskurve der Leistungskurve.
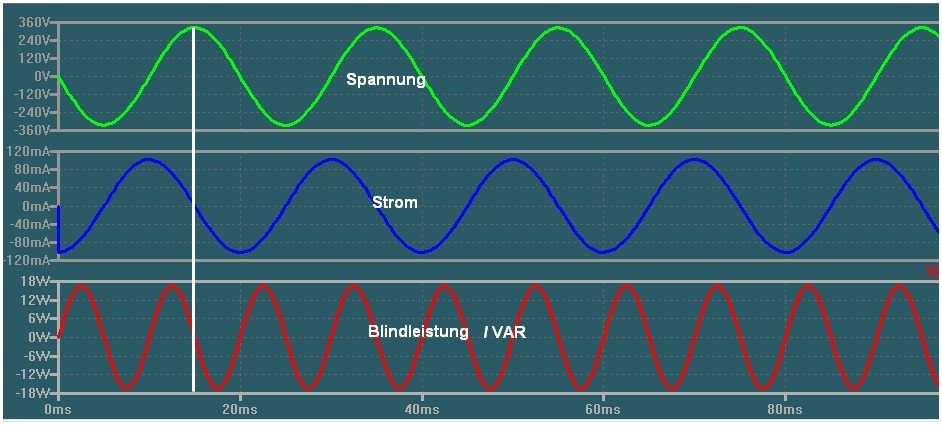
Im Diagramm unten erkennt man jetzt an der Position der weißen senkrechten Linie eine
Verschiebung der Sinuswellen.
Durch diese Verschiebung ergibt die momentane Multiplikation von Spannung und Strom
immer den Wert Null.
Deutlich erkennt man es im untersten Diagramm , denn dort hat die Leistungskurve immer
eine wechselnde
Leistung im Positiven wie auch im Negativen Bereich.
Dadurch hebt sich der Leistungsverbrauch auf.
Diese Leistung pendelt immer nur zwischen Verbraucher und Erzeuger hin und her und
erzeugt somit keinerlei Arbeit.
Was diese Leistung aber verursacht sind Leitungsverluste.
Weil die Leistung aber keine Arbeit verrichtet bezeichnet man sie als Blindleistung und ist eigentlich ungewollt.
Die Angabe der Blindleistung ist VAR.
Das der Kondensator keine Leistung verbraucht erkennt man schon daran, das er nicht warm wird.
Im ersten Beispiel beim
rein Ohmschen Verbraucher lagen Spannung und Strom ingleicher Phase an und erzeugten eine Wirkleistung (P).
Im zweiten Beispiel beim Kondensator lag eine Phasenverschiebung vor, dann
sprechen wir von einer Blindleistung(Q).
Werden jetzt wie hier dargestellt beiden Schaltungen miteinander kombiniert,also
ein kapazitiver und ein ohmscher Verbraucher dann liegt eine Wirkleistung und
eine Blindleistung vor.
Die Addition dieser beiden Leistungen ist die Scheinleistung (S).
Um es verständlicher zu machen wird oft das Beispiel eines Bier gefüllten Glase genommen.
Der Inhalt, das Bier ist dann die Wirkleistung das also was eine Wirkung erzielt ,
während der darauf enthaltende Schaum der Blindleistung entspricht also das was
keinen Nutzen erfüllt.
Beides zusammen ist die Scheinleistung die übertragen und auch wie beim Bier bezahlt werden muss.
Eine Phasenverschiebung tritt aber nicht
nur beim Kondensator sondern auch in einerSpule auf.
Beim Kondensator eilt der Strom der Spannung um 90° voraus.
Bei einer Spule ist es umgekehrt, da hinkt der Strom der Spannung um 90° hinterher.
Lege ich ich nun eine Spule parallel zum Kondensator dann heben sich diese beiden
Verschiebungen gegeneinander auf.
Man spricht dann von einer Kompensation.
Habe ich beispielsweise einen Kondensator mit einer Kapazität von 10uF, und
möchte die damit einhergehende Phasenverschiebung aufheben, benötige ich ein
parallel liegende Spule von 1000 mH.
Beide Bauteile müssen den gleichen Blindwiderstand entsprechen.
Angenommen es befindet sich eine Induktivität in meiner Schaltung ( 50 Hz , 230V) mit einen Wert von 1 Henry.
Benötige ich zu erst den Blindwiderstand der Induktivität.
Rx = 2 * Pie * f * L
Rx = 2 * 3,14 * 50 Hz * 1 Henry
Rx = 314 Ohm
Dann wird als Kapazität ein Kondensator mit dem gleichen Blindwiderstand benötigt
C= 1/ (50Hz* 314 Ohm * 2*Pie)
C= 10 uF
| Leuchtkörper | Volt | A | Watt | VA | Cos |
| Led | 231 | 0,041 | 6,0 | 9,6 | 0,62 |
| Sparbirne | 231 | 0,071 | 10,8 | 16,4 | 0,66 |
| Glühbirne | 231 | 0,094 | 21,9 | 21,9 | 1,0 |
Aktualisiert
26.06.2024