erstellt  21.10.2012

Schwingkreis berechnen

Als Schwingkreis bezeichnet man im einfachsten Fall die Anordnung eines Kondensators und einer Spule in einem geschlossenen Stromkreis. Durch das Anlegen einer äußeren Wechselspannung kann ein Schwingkreis zu elektromagnetischen Eigenschwingungen angeregt werden. Bei diesen Schwingungen wandeln sich beständig elektrische Feldenergie im Kondensator und magnetische Feldenergie an der Spule um.

Würden sich in einem Schwingkreis nur der kapazitive Widerstand des Kondensators und der induktive Widerstand der Spule befinden, dann müsste der Schwingungsvorgang ohne Verluste unaufhörlich vonstatten gehen. Die Amplitude der elektromagnetischen Schwingung würde nicht abnehmen, die Schwingung selbst wäre also ungedämpft. Diese Eigenschaft hängt mit dem Verhalten kapazitiver und induktiver Widerstände zusammen die, anders als ohmsche Widerstände, keine elektromagnetische Energie in thermische Energie umwandeln. Die Periodendauer einer elektromagnetischen Schwingung im ungedämpften Schwingkreis hängt nur von der Kapazität C des Kondensators und der Induktivität L der Spule ab. 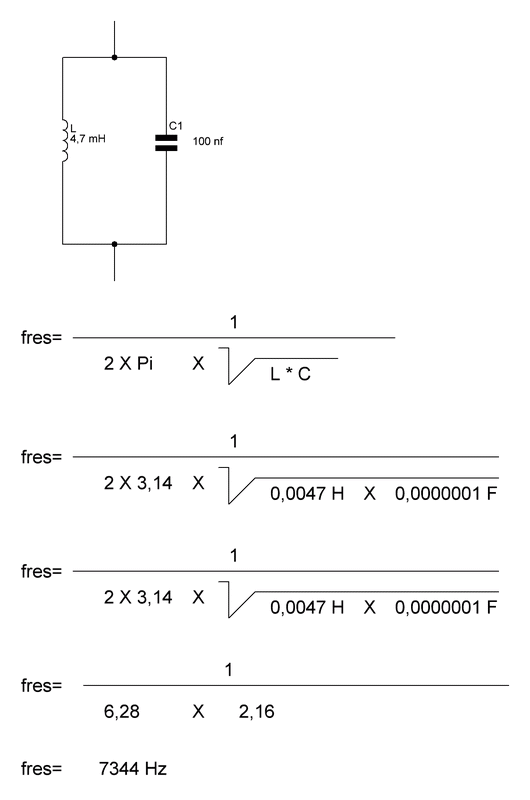Man berechnet die Periodendauer mit einer Gleichung, die als Thomsonsche Schwingungsgleichung bezeichnet wird:

Bei dieser Formel wird nur der Frequenzabhängige Widerstand berechnet, der reine Gleichstromwiderstand der Induktivität wird dabei außer acht gelassen weil er für die meisten Anwendungen keine all zu große Bedeutung hat.

Eine Spule und ein Kondensator verhalten sich im Wechselstromkreis gegensinnig. Um das zu verdeutlichen übertreiben wir einmal und sehen uns Spule und Kondensator bei einer Wechselspannung von 0 Herz an und dann bei einer Frequenz von unendlich hoch. Bei einer Frequenz von 0 Herz also gleichbedeutend mit Gleichspannung hat eine Spule einen Widerstand von fast Null Ohm,der Kondensator hingegen einen sehr großen Widerstand.  Dadurch fließt der Strom fast ausschließlich durch die Spule. Bei einer sehr hohen Frequenz wird der Strom in der Spule stark gedrosselt , hingegen fließt er nun durch den Kondensator hindurch. Bei einer mittleren Frequenz aber fließt der Strom zu gleichen Teile in der Spule sowie durch den Kondensator. Und genau diese Frequenz bei der ein Gleichgewicht zwischen Kapazitiven und Induktiven Widerstand besteht nennt man Resonanzfrequenz.

Beispiel:

L = 0,6 mH, C = 200 pF, f0 =  459 kHz L = 0,3 H, C = 15 μF, f0 = 75 Hz L = 0,5 H, C = 4,5 μF, f0 = 106 Hz

Die Wellenlänge berechnet sich aus der Lichtgeschwindigkeit ( 300 000  000 m/s) durch die Frequenz . Beispiel : Kondensator = 400 pf Spule = 200 uH = ca.562 KHz =533 Meter

aktualisiert 21.10.2012